Ik heb het in dit artikel niet over films met wiskundige thema’s of wiskundigen als personages. Het gaat meer over hoe wiskunde mee aan de grond ligt van een van de grootste evoluties in de filmgeschiedenis, en hoe het een steeds belangrijkere factor speelt in deze industrie. Als we de lijsten met kaskrakers bekijken vinden we steeds meer animatiefilms terug (denk maar aan cars, wall-e, shrek,…). Deze films hadden allemaal veel minder indrukwekkend geweest indien de hoofdpersonage’s niet realistisch zouden overkomen. Het is hier waar de Wiskunde een belangrijke rol begint te spelen.
Laten we even bij het begin beginnen. Iedereen meent te denken dat een cirkel geen hoeken heeft…. maar is dat wel zo? Voor een cirkel zoals we ze in de wiskunde beschrijven en gebruiken wel, maar hoe tekent bijvoorbeeld een computer een cirkel? Wel eigenlijk begint deze met een regelmatige veelhoek (een veelhoek met gelijke zijden én gelijke hoeken). Maar gebruikt de computer dan een 3-hoek, 4-hoek, 15-hoek… Wel dat hangt een beetje van de software af natuurlijk, maar hoe meer hoeken je gebruikt hoe meer je veelhoek op een cirkel begint te lijken:
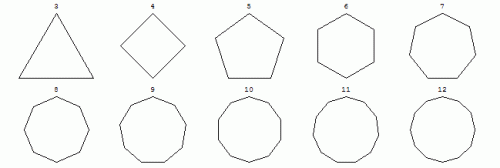
Inderdaad, we kunnen met het blote oog nog zien dat de 12-hoek inderdaad nog geen cirkel is, maar je begrijpt het idee wel. Indien we een cirkel net naast een regelmatige 100-hoek zouden plaatsen zou het voor ons al veel moeilijker zijn om te onderscheiden welke van de 2 nu de echte cirkel is en de welke de veelhoek. Per definitie kan je eigenlijk zeggen dat de cirkel een regelmatige ∞-hoek (oneindig-hoek) is. Vele benaderingen van het getal π (zowat het belangrijkste wiskundige getal en onlosmakend verbonden met cirkels) zijn gebaseerd op die laatste definitie.
Maar zoals gezegd was dat slechts het begin, in 2 dimensies. Maar de nieuwe generatie tekenfilms brengt ons alles in 3D.
In 2D voegden we hoeken en zijden toe om de figuur tot een vloeiende cirkel te maken, kunnen we dit principe toepassen op 3D figuren? Ja, en wel op verschillende manieren. Deze methoden worden ook wel “oppervlakte onderverdelingen” genoemd (je zal meteen weten waarom). Laten we even volgende voorbeeld nemen waar een kubus ‘ronder en ronder’ gemaakt wordt tot het een bal is:
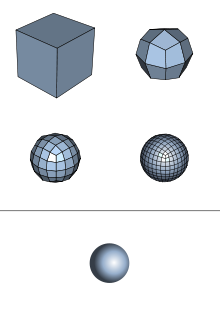
Natuurlijk is dit slechts één voorbeeld van een 3D figuur. Wanneer we complexere figuren bekijken passen we echter steeds hetzelfde systeem toe. Eerst beginnen we met een afgevlakte figuur, die we vrij makkelijk kunnen maken met reeds bestaande computerprogramma’s. Deze afgevlakte figuur is alles behalve realistisch dus we zullen ze moeten afronden… Wel we verdelen van de afgevlakte figuur elke zijde in kleinere deeltjes (In het 2D voorbeeld met de cirkel voegden we zijden (1D) toe aan de veelhoek, in dit 3D voorbeeld voegen we veelhoeken (2D) toe aan de kubus). Het is door deze stap dat we de methodes ook wel “oppervlakte onderverdeling” noemen, omdat we de oppervlakten van de zijdes onderverdelen in kleinere veelhoeken. Die deeltjes kunnen we dan een klein beetje draaien ten opzichte van elkaar waardoor de figuur meer afgerond lijkt. Als we dan met die figuur de stap herhalen lijkt de figuur nog beter afgerond,….. Na vele stappen zal de figuur realistischer lijken, zoals te zien in volgende voorbeeld:
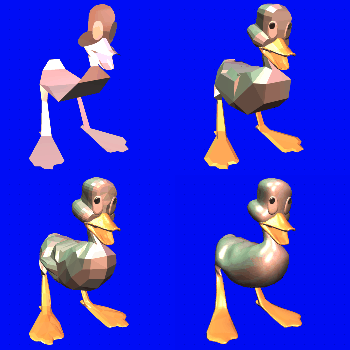
Hier zie je ook nog een mooi voorbeeld, het verschil in de figuren is dat we 60/600/6000 of 60000 driehoeken gebruiken: 
Er zijn verschillende manieren om dit concept toe te passen. Ze verschillen vooral in de manier waarop we de zijden onderverdelen in kleinere deeltjes. Het ene systeem deelt bijvoorbeeld alle zijden op in driehoeken, de andere in vierhoeken,… Ook de manier waarop de nieuwe deeltjes een beetje gedraaid worden verschilt tussen verschillende systemen. De belangrijkste 3 systemen zijn Catmill-Clarck-systeem, Doo-Sabin-systeem en de methode van Loop.
Ook in computerspellen merken we deze evolutie natuurlijk!!!

DAAROM WISKUNDE
Giedts Tom
